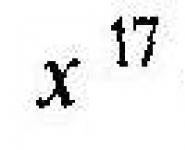Знаменник геом прогресії дорівнює 1 3. Геометрична прогресія та її формула. Властивості геометричної прогресії

А ви знаєте дивовижну легенду про зернах на шаховій дошці?

Легенда про зернах на шаховій дошці

Коли творець шахів (давньоіндійський математик по імені Сесса) показав свій винахід правителю країни, тому так сподобалася гра, що він дозволив винахіднику право самому вибрати нагороду. Мудрець попросив у короля за першу клітину шахівниці заплатити йому одне зерно пшениці, за друге - два, за третє - чотири і т. Д., Подвоюючи кількість зерен на кожній наступній клітці. Правитель, що не розбирався в математиці, швидко погодився, навіть кілька образившись на таку невисоку оцінку винаходу, і наказав скарбнику підрахувати і видати винахіднику потрібну кількість зерна. Однак, коли через тиждень скарбник все ще не зміг підрахувати, скільки потрібно зерен, відповів і сказав, у чому причина такої затримки. Скарбник показав йому розрахунки і сказав, що розплатитися невозможно.С подивом слухав цар словами старця.

Назви ж мені це жахливе число, - сказав він.

18 квінтильйонів 446 квадрильйонів 744 трильйона 73 більйона 709 мільйонів 551 тисяча 615, о повелитель!

Якщо прийняти, що одне зернятко пшениці має масу 0,065 грама, тоді загальна маса пшениці на шахівниці складе 1,200 трильйонів тонн, що перевищує весь обсяг врожаю пшениці, зібраний за всю історію людства!

визначення

Геометрична прогресія - послідовність чисел ( членів прогресії), В якій кожне наступне число, починаючи з другого, виходить з попереднього множенням його на певне число ( знаменник прогресії):

Наприклад, послідовність 1, 2, 4, 8, 16, ... - геометрична ()

Геометрична прогресія

Знаменник геометричної прогресії

Характеристичне властивість геометричної прогресії

Для title \u003d "(! LANG: Rendered by QuickLaTeX.com" height="15" width="48" style="vertical-align: -1px;">!}

Послідовність є геометричній тоді і тільки тоді, коли для будь-якого n\u003e 1 виконується вказане вище співвідношення.

Зокрема, для геометричної прогресії з позитивними членами, вірно:

Формула n-го члена геометричної прогресії

Сума n перших членів геометричної прогресії

(Якщо ж, то)

Нескінченно спадна геометрична прогресія

При, геометрична прогресія називається нескінченно спадної . Сумою нескінченно спадної геометричної прогресії називається число і

приклади

приклад 1.

Послідовність () -геометріческая прогресія.

Знайдіть, якщо,

Рішення:

Відповідно до формули маємо:

Пріметр 2.

Знайдіть знаменник геометричної прогресії (), в якій

наприклад, Послідовність \\ (3 \\); \\ (6 \\); \\ (12 \\); \\ (24 \\); \\ (48 \\) ... є геометричною прогресією, тому що кожен наступний елемент відрізняється від попереднього в два рази (інакше кажучи, може бути отриманий з попереднього множенням його на два):

Як і будь-яку послідовність, геометричну прогресію позначають маленької латинською літерою. Числа, що утворюють прогресію, називають її членами (Або елементами). Їх позначають тією ж буквою, що і геометричну прогресію, але з числовим індексом, рівним номеру елемента по порядку.

наприклад, Геометрична прогресія \\ (b_n \u003d \\ (3; 6; 12; 24; 48 ... \\) \\) складається з елементів \\ (b_1 \u003d 3 \\); \\ (B_2 \u003d 6 \\); \\ (B_3 \u003d 12 \\) і так далі. Іншими словами:

Якщо ви зрозуміли вищевикладену інформацію, то вже зможете вирішити більшість завдань на цю тему.

Приклад (ОГЕ):
Рішення:

відповідь : \(-686\).

Приклад (ОГЕ): Дано перші три члена прогресії \\ (324 \\); \\ (- 108 \\); \\ (36 \\) .... Знайдіть \\ (b_5 \\).
Рішення:

	Щоб продовжити послідовність, нам потрібно знати знаменник. Знайдемо його з двох сусідніх елементів: на що потрібно помножити \\ (324 \\), щоб вийшло \\ (- 108 \\)?
\\ (324 · q \u003d -108 \\)	Звідси без проблем обчислюємо знаменник.
\\ (Q \u003d - \\) \\ (\\ frac (108) (324) \\) \\ (\u003d - \\) \\ (\\ frac (1) (3) \\)	Тепер ми легко знаходимо потрібний нам елемент.
	Готовий відповідь.

відповідь : \(4\).

приклад: Прогресія задана умовою \\ (b_n \u003d 0,8 · 5 ^ n \\). Яке з чисел є членом цієї прогресії:

а) \\ (- 5 \\) б) \\ (100 \\) в) \\ (25 \\) г) \\ (0,8 \\)?

Рішення: З формулювання завдання очевидно, що одне з цих чисел точно є в нашій прогресії. Тому ми можемо просто обчислювати її члени по черзі, поки не знайдемо потрібне нам значення. Так як у нас прогресія задана формулою, то обчислюємо значення елементів, підставляючи різні \\ (n \\):
\\ (N \u003d 1 \\); \\ (B_1 \u003d 0,8 · 5 ^ 1 \u003d 0,8 · 5 \u003d 4 \\) - такого числа в списку немає. Продовжуємо.
\\ (N \u003d 2 \\); \\ (B_2 \u003d 0,8 · 5 ^ 2 \u003d 0,8 · 25 \u003d 20 \\) - і цього теж немає.
\\ (N \u003d 3 \\); \\ (B_3 \u003d 0,8 · 5 ^ 3 \u003d 0,8 · 125 \u003d 100 \\) - а ось і наш чемпіон!

відповідь: \(100\).

Приклад (ОГЕ): Дано кілька йдуть послідовно один за одним членів геометричної прогресії ... \\ (8 \\); \\ (X \\); \\ (50 \\); \\ (- 125 \\) .... Знайдіть значення елемента, позначеного літерою \\ (x \\).

Рішення:

відповідь: \(-20\).

Приклад (ОГЕ): Прогресія задана умовами \\ (b_1 \u003d 7 \\), \\ (b_ (n + 1) \u003d 2b_n \\). Знайдіть суму перших \\ (4 \\) членів цієї прогресії.

Рішення:

відповідь: \(105\).

Приклад (ОГЕ): Відомо, що в геометричній прогресії \\ (b_6 \u003d -11 \\), \\ (b_9 \u003d 704 \\). Знайдіть знаменник \\ (q \\).

Рішення:

	Зі схеми зліва видно, що щоб «потрапити» з \\ (b_6 \\) в \\ (b_9 \\) - ми робимо три «кроку», тобто три рази множимо \\ (b_6 \\) на знаменник прогресії. Іншими словами \\ (b_9 \u003d b_6 · q · q · q \u003d b_6 · q ^ 3 \\).
\\ (B_9 \u003d b_6 · q ^ 3 \\)	Підставами відомі нам значення.
\\ (704 \u003d (- 11) · q ^ 3 \\)	«Перевернемо» рівняння і розділимо його на \\ ((- 11) \\).
\\ (Q ^ 3 \u003d \\) \\ (\\ frac (704) (- 11) \\) \\ (\\: \\: \\: ⇔ \\: \\: \\: \\) \\ (q ^ 3 \u003d - \\) \\ (64 \\)	Яке число в кубі дасть \\ (- 64 \\)? Звичайно, \\ (- 4 \\)!
	Відповідь знайдений. Його можна перевірити, відновивши ланцюжок чисел від \\ (- 11 \\) до \\ (704 \\).
	Все зійшлося - відповідь вірний.

відповідь: \(-4\).

найважливіші формули

Як бачите, більшість завдань на геометричну прогресію можна вирішувати чистої логікою, просто розуміючи суть (це взагалі характерно для математики). Але іноді знання деяких формул і закономірностей прискорює і істотно полегшує вирішення. Ми вивчимо дві такі формули.

Формула \\ (n \\) - го члена: \\ (b_n \u003d b_1 · q ^ (n-1) \\), де \\ (b_1 \\) - перший член прогресії; \\ (N \\) - номер шуканого елемента; \\ (Q \\) - знаменник прогресії; \\ (B_n \\) - член прогресії з номером \\ (n \\).

За допомогою цієї формули можна, наприклад, вирішити задачу з самого першого прикладу буквально в одну дію.

Приклад (ОГЕ): Геометрична прогресія задана умовами \\ (b_1 \u003d -2 \\); \\ (Q \u003d 7 \\). Знайдіть \\ (b_4 \\).
Рішення:

відповідь: \(-686\).

Цей приклад був простим, тому формула нам полегшила обчислення не дуже сильно. Давайте розберемо завдання трохи складніше.

приклад: Геометрична прогресія задана умовами \\ (b_1 \u003d 20480 \\); \\ (Q \u003d \\ frac (1) (2) \\). Знайдіть \\ (b_ (12) \\).
Рішення:

відповідь: \(10\).

Звичайно, зводити \\ (\\ frac (1) (2) \\) в \\ (11 \\) - ую ступінь не дуже радісно, \u200b\u200bале все ж простіше ніж \\ (11 \\) раз ділити \\ (20480 \\) на два.

Сума \\ (n \\) перших членів: \\ (S_n \u003d \\) \\ (\\ frac (b_1 · (q ^ n-1)) (q-1) \\), де \\ (b_1 \\) - перший член прогресії; \\ (N \\) - кількість сумміруемих елементів; \\ (Q \\) - знаменник прогресії; \\ (S_n \\) - сума \\ (n \\) перших членів прогресії.

Приклад (ОГЕ): Дана геометрична прогресія \\ (b_n \\), знаменник якої дорівнює \\ (5 \\), а перший член \\ (b_1 \u003d \\ frac (2) (5) \\). Знайдіть суму перших шести членів цієї прогресії.
Рішення:

відповідь: \(1562,4\).

І знову ми могли вирішити задачу «в лоб» - знайти по черзі всі шість елементів, а потім скласти результати. Однак кількість обчислень, а значить і шанс випадкової помилки, різко зросли б.

Для геометричній прогресії є ще кілька формул, які ми не стали розглядати тут через їх низьку практичної користі. Ви можете знайти ці формули.

Зростаючі і спадні геометричні прогресії

У розглянутої на самому початку статті прогресії \\ (b_n \u003d \\ (3; 6; 12; 24; 48 ... \\) \\) знаменник \\ (q \\) більше одиниці і тому кожен наступний член більше попереднього. Такі прогресії називаються зростаючими.

Якщо ж \\ (q \\) менше одиниці, але при цьому позитивний (тобто, лежить в межах від нуля до одиниці), то кожен наступний елемент буде менше ніж попередній. Наприклад, в прогресії \\ (4 \\); \\ (2 \\); \\ (1 \\); \\ (0,5 \\); \\ (0,25 \\) ... знаменник \\ (q \\) дорівнює \\ (\\ frac (1) (2) \\).

Ці прогресії називаються убутними. Зверніть увагу, що жоден з елементів такої прогресу не буде негативний, вони просто стають все менше і менше з кожним кроком. Тобто, ми будемо поступово наближатися до нуля, але ніколи його не досягнемо і за нього не перейдемо. Математики в таких випадках кажуть «прагнути до нуля».

Відзначимо, що при негативному знаменнику елементи геометричної прогресії будуть обов'язково міняти знак. наприклад, У прогресії \\ (5 \\); \\ (- 15 \\); \\ (45 \\); \\ (- 135 \\); \\ (675 \\) ... знаменник \\ (q \\) дорівнює \\ (- 3 \\), і через це знаки елементів «блимають».

геометричною прогресією називається послідовність чисел, в якій кожен член (починаючи з другого) виходить з попереднього шляхом множення його на одного і того ж число q ≠ 0. Число q називають знаменником геометричній прогресії. Для того, щоб задати геометричну прогресію, потрібно задати її перший член a 1 і знаменник q.

Геометрична прогресія зростає при q\u003e 1, зменшується при 0< q < 1.

Приклади геометричних прогресій:

1. 2, 4, 8, 16 .... Тут перший член дорівнює 1, а знаменник дорівнює 2.

81, 27, 9, 3, 1, 1/3 .... Тут перший член дорівнює 81, а знаменник дорівнює 1/3.

Отже, перший член прогресії дорівнює a 1, другий - a 1 q, третій a 1 q * q \u003d a 1 q 2, четвертий a 1 q 2 * q \u003d a 1 q 3 .... Таким чином, n-й член прогресії обчислюється за формулою a n \u003d a 1 q n-1.

затвердження: Сума n членів геометричної прогресії обчислюється за формулою

S n \u003d a 1 + a 1 q + a 1 q 2 + a 1 q 3 + ... + a 1 q n-1.

Помножимо на, отримаємо:

S n q \u003d a 1 q + a 1 q 2 + a 1 q 3 + ... a 1 q n.

Тепер віднімемо S n q з S n.

Приклади завдань на геометричну прогресію.

1. Знайдіть суму перших 10 членів геометричної прогресії, якщо відомо, що a 1 \u003d 3, q \u200b\u200b\u003d 4.

2. За одну хвилину біомаса збільшується в 2 рази. Яку вагу вона матиме через 5 хвилин, якщо зараз її вага 3 кг.

Ми маємо справу з геометричною прогресією, у якій a 1 \u003d 3, а q \u003d 2 Щоб вирішити задачу, нам потрібно знайти шостий член цієї прогресії.

Розглянемо деякий ряд.

7 28 112 448 1792...

Абсолютно ясно видно, що значення будь-якого його елемента більше попереднього рівно в чотири рази. Значить, даний ряд є прогресією.

Геометричній прогрессіейіменуется нескінченна послідовність чисел, головною особливістю якої є те, що наступне число виходить з попереднього за допомогою множення на якесь певне число. Це виражається наступною формулою.

a z +1 \u003d a z · q, де z - номер обраного елемента.

Відповідно, z ∈ N.

Період, коли в школі вивчається геометрична прогресія - 9 клас. Приклади допоможуть розібратися в понятті:

0.25 0.125 0.0625...

Виходячи з цієї формули, знаменник прогресії можливо визначити наступним чином:

Ні q, ні b z не можуть дорівнювати нулю. Так само кожен з елементів прогресії не повинен дорівнювати нулю.

Відповідно, щоб дізнатися наступне число ряду, потрібно помножити останнім на q.

Щоб задати дану прогресію, необхідно вказати перший її елемент і знаменник. Після цього можливе знаходження будь-якого з наступних членів і їх суми.

різновиди

Залежно від q і a 1, дана прогресія розділяється на кілька видів:

• Якщо і a 1, і q більше одиниці, то така послідовність - зростаюча з кожним наступним елементом геометрична прогресія. Приклад такої представлений далі.

Приклад: a 1 \u003d 3, q \u200b\u200b\u003d 2 - обидва параметри більше одиниці.

Тоді числова послідовність може бути записана так:

3 6 12 24 48 ...

• Якщо | q | менше одиниці, тобто, множення на нього еквівалентно поділу, то прогресія з подібними умовами - спадна геометрична прогресія. Приклад такої представлений далі.

Приклад: a 1 \u003d 6, q \u003d 1/3 - a 1 більше одиниці, q - менше.

Тоді числову послідовність можна записати таким чином:

6 2 2/3 ... - будь-який елемент більше елемента, наступного за ним, в 3 рази.

• Знакозмінна. якщо q<0, то знаки у чисел последовательности постоянно чередуются вне зависимости от a 1 , а элементы ни возрастают, ни убывают.

Приклад: a 1 \u003d -3, q \u003d -2 - обидва параметри менше нуля.

Тоді числову послідовність можна записати так:

3, 6, -12, 24,...

формули

Для зручного використання геометричних прогресій існує безліч формул:

• Формула z-го члена. Дозволяє розрахувати елемент, що стоїть під конкретним номером без розрахунку попередніх чисел.

приклад:q = 3, a 1 \u003d 4. Потрібно порахувати четвертий елемент прогресії.

Рішення:a 4 = 4 · 3 4-1 = 4 · 3 3 = 4 · 27 = 108.

• Сума перших елементів, чия кількість одно z. Дозволяє розрахувати суму всіх елементів послідовності доa z включно.

Так як (1q) Коштує в знаменнику, то (1 - q)≠ 0, отже, q не дорівнює 1.

Зауваження: якщо б q \u003d 1, то прогресія представляла б собою ряд з нескінченно повторюваного числа.

Сума геометричній прогресії, приклади:a 1 = 2, q \u003d -2. Порахувати S 5.

Рішення:S 5 = 22 - розрахунок за формулою.

• Сума, якщо |q| < 1 и если z стремится к бесконечности.

приклад:a 1 = 2 , q \u003d 0.5. Знайти суму.

Рішення:S z = 2 · = 4

S z = 2 + 1 + 0.5 + 0.25 + 0.125 + 0.0625 = 3.9375 4

Деякі властивості:

• Характеристичне властивість. Якщо така умова виконується для будь-якогоz, То заданий числовий ряд - геометрична прогресія:

a z 2 = a z -1 · a z + 1

• Так само квадрат будь-якого числа геометричній прогресії знаходиться за допомогою додавання квадратів двох інших будь-яких чисел в заданому ряду, якщо вони рівновіддалені від цього елемента.

a z 2 = a z - t 2 + a z + t 2 , деt - відстань між цими числами.

• елементи розрізняються в qраз.
• Логарифми елементів прогресії так само утворюють прогресію, але вже арифметичну, тобто кожен з них більше попереднього на певне число.

Приклади деяких класичних задач

Щоб краще зрозуміти, що таке геометрична прогресія, приклади з рішенням для 9 класу можуть допомогти.

• умови:a 1 = 3, a 3 \u003d 48. Знайтиq.

Рішення: кожен наступний елемент більше попереднього вq раз.Необхідно висловити одні елементи через інші за допомогою знаменника.

отже,a 3 = q 2 · a 1

при підстановціq= 4

• умови:a 2 = 6, a 3 \u003d 12. Розрахувати S 6.

Рішення:Для цього достатньо знайти q, перший елемент і підставити в формулу.

a 3 = q· a 2 , Отже,q= 2

a 2 \u003d q · A 1,тому a 1 \u003d 3

S 6 \u003d 189

• · a 1 = 10, q \u003d -2. Знайти четвертий елемент прогресії.

Рішення: для цього достатньо висловити четвертий елемент через перший і через знаменник.

a 4 \u003d q 3· a 1 \u003d -80

Приклад застосування:

• Клієнт банку зробив внесок на суму 10000 рублів, за умовами якого щороку клієнту до основної суми будуть додаватися 6% від неї ж. Скільки коштів буде на рахунку через 4 роки?

Рішення: Початкова сума дорівнює 10 тисячам рублів. Значить, через рік після вкладення на рахунку буде сума, рівна 10000 + 10000 · 0.06 \u003d 10000 · 1.06

Відповідно, сума на рахунку ще через один рік виражатиметься наступним чином:

(10000 · 1.06) · 0.06 + 10000 · 1.06 \u003d 1.06 · 1.06 · 10000

Тобто з кожним роком сума збільшується в 1.06 раз. Значить, щоб знайти кількість коштів на рахунку через 4 роки, досить знайти четвертий елемент прогресії, яка задана першим елементом, рівним 10 тисячам, і знаменником, рівним 1.06.

S \u003d 1.06 · 1.06 · 1.06 · 1.06 · 10000 \u003d 12625

Приклади завдань на обчислення суми:

У різних завданнях використовується геометрична прогресія. Приклад на знаходження суми може бути заданий наступним чином:

a 1 = 4, q \u003d 2, розрахуватиS 5.

Рішення: всі необхідні для розрахунку дані відомі, потрібно просто підставити їх в формулу.

S 5 = 124

• a 2 = 6, a 3 \u003d 18. Розрахувати суму перших шести елементів.

Рішення:

У геом. прогресії кожен наступний елемент більше попереднього в q разів, тобто для обчислення суми необхідно знати елементa 1 і знаменникq.

a 2 · q = a 3

q = 3

Аналогічним чином потрібно знайтиa 1 , знаючиa 2 іq.

a 1 · q = a 2

a 1 \u003d2

S 6 = 728.

Геометрична прогресія - це числова послідовність, перший член якої відмінний від нуля, а кожен наступний член дорівнює попередньому члену, помноженому на одне й те саме не рівне нулю число. Геометрична прогресія позначається b1, b2, b3, ..., bn, ...

Властивості геометричної прогресії

Ставлення будь-якого члена геометричної похибки до її попереднього члену дорівнює одному й тому числу, тобто b2 / b1 \u003d b3 / b2 \u003d b4 / b3 \u003d ... \u003d bn / b (n-1) \u003d b (n + 1) / bn \u003d .... Це випливає безпосередньо з визначення арифметичній прогресії. Це число називають знаменником геометричної прогресії. Зазвичай знаменник геометричній прогресії позначають буквою q.

Одним із способів завдання геометричної прогресії є завдання її першого члена b1 і знаменника геометричній похибки q. Наприклад, b1 \u003d 4, q \u003d -2. Ці дві умови задають геометричну прогресію 4, -8, 16, -32, ....

Якщо q\u003e 0 (q не дорівнює 1), то прогресія є монотонною послідовністю. Наприклад, послідовність, 2, 4,8,16,32, ... є монотонно зростаючою послідовністю (b1 \u003d 2, q \u003d 2).

Якщо в геометричній похибки знаменник q \u003d 1, то всі члени геометричної прогресії будуть рівні між собою. У таких випадках кажуть, що прогресія є постійною послідовністю.

Формула n-го члена прогресії

Для того, щоб числова послідовність (bn) була геометричною прогресією необхідно, щоб кожен її член, починаючи з другого, був середнім геометричним сусідніх членів. Тобто необхідним є дотримання наступного рівняння - (b (n + 1)) ^ 2 \u003d bn * b (n + 2), для будь-якого n\u003e 0, де n належить множині натуральних чисел N.

Формула n-ого члена геометричної прогресії має вигляд:

bn \u003d b1 * q ^ (n-1), де n належить множині натуральних чисел N.

Розглянемо простий приклад:

У геометричній прогресії b1 \u003d 6, q \u003d 3, n \u003d 8 знайти bn.

Скористаємося формулою n-ого члена геометричної прогресії.