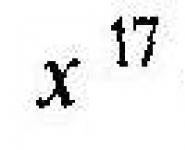Визначити критичні точки функції онлайн. Екстремум функції. необхідною умовою екстремуму
Це досить-таки цікавий розділ математики, з яким стикаються абсолютно всі учні випускних класів та студенти. Проте далеко не кожному подобається матан. Деякі не можуть зрозуміти навіть елементарних речей на зразок, здавалося б, стандартного дослідження функції. Дана стаття покликана виправити подібну помилку. Хочете детальніше дізнатися про аналіз функції? Бажаєте дізнатися, що таке точки екстремуму і як їх знайти? Тоді дана стаття для вас.
Дослідження графіка функції
Для початку варто зрозуміти, навіщо взагалі необхідно аналізувати графік. Існують прості функції, накреслити які не складе труднощів. Яскравим прикладом подібної функції може служити парабола. Накреслити її графік не складе труднощів. Все що необхідно, так це за допомогою простого перетворення знайти числа, при яких функція приймає значення 0. І в принципі це все що знати для того, щоб накреслити графік параболи.
Але що робити, якщо функція, графік якої нам потрібно накреслити, набагато складніше? Оскільки властивості складних функцій досить-таки неочевидні, необхідно проводити цілий аналіз. Тільки після цього можна зобразити функцію графічно. Як же це зробити? Відповідь на це питання ви зможете знайти в даній статті.
План аналізу функції
Перше, що необхідно зробити, так це провести поверхневе дослідження функції, в ході якого ми знайдемо область визначення. Отже, почнемо по порядку. Область визначення - це сукупність тих значень, якими функція задається. Простіше кажучи, це ті числа, які можна використовувати в функції замість х. Для того щоб визначити область визначення, необхідно просто поглянути на запис. Наприклад, очевидно, що у функції у (х) \u003d х 3 + х 2 - х + 43 область визначення - безліч дійсних чисел. Ну а з функцією зразок (х 2 - 2х) / х все трохи інакше. Оскільки число в знаменнику не повинно дорівнювати 0, то областю визначення даної функції будуть всі дійсні числа, крім нуля.
Далі необхідно знайти так звані нулі функції. Це ті значення аргументу, при яких вся функція приймає значення нуль. Для цього необхідно прирівняти функцію до нуля, докладно її розглянути і зробити деякі перетворення. Візьмемо вже знайому нам функцію у (х) \u003d (х 2 - 2х) / х. Зі шкільного курсу ми знаємо, що дріб дорівнює 0 тоді, коли чисельник дорівнює нулю. Тому знаменник ми відкидаємо і починаємо працювати з чисельником, прирівнюючи його до нуля. Отримуємо х 2 - 2х \u003d 0 і виносимо х за скобочки. Звідси х (х - 2) \u003d 0. В результаті отримуємо, що наша функція дорівнює нулю тоді, коли х дорівнює 0 або ж 2.
Під час дослідження графіка функції багато стикаються з проблемою у вигляді точок екстремуму. І це дивно. Адже екстремуми - це досить-таки проста тема. Не вірите? Переконайтеся самі, прочитавши цю частину статті, в якій ми поговоримо про точках мінімуму і максимуму.

Для початку варто розібратися в тому, що собою являє екстремум. Екстремум - це граничне значення, яке досягає функція на графіку. Звідси виходить, що існує два крайніх значення - максимум і мінімум. Для наочності можна подивитися на картинку, що розташована вище. На дослідженій області точка -1 є максимумом функції у (х) \u003d х 5 - 5х, а точка 1, відповідно, мінімумом.
Також не варто плутати між собою поняття. Точки екстремуму функції - це ті аргументи, при яких задана функція набуває крайні значення. У свою чергу, екстремумів називають значення мінімумів і максимумів функції. Наприклад, знову розглянемо малюнок вище. -1 і 1 - це точки екстремуму функції, а 4 і -4 - це самі екстремуми.
Знаходження точок екстремуму

Але як все-таки знайти точки екстремуму функції? Все досить-таки просто. Перше, що необхідно зробити - знайти похідну рівняння. Припустимо, ми отримали завдання: "Знайдіть точки екстремуму функції y (x), x - аргумент. Для наочності візьмемо функцію у (х) \u003d х 3 + 2х 2 + х + 54. Проведемо диференціювання і отримаємо наступне рівняння: 3х 2 + 4х + 1. В результаті ми отримали стандартне квадратне рівняння. Все, що необхідно зробити далі - прирівняти його до нуля і знайти коріння. Оскільки дискримінант більше нуля (D \u003d 16 - 12 \u003d 4), дане рівняння визначається двома країнами. Знаходимо їх і отримуємо два значення: 1/3 і -1. Це і будуть точки екстремуму функції. Однак як все-таки визначити, хто є хто? яка точка є максимумом, а яка мінімумом? Для цього потрібно взяти сусідню точку і дізнатися її значення. наприклад , візьмемо число -2, яке знаходиться зліва по координатної прямої від -1. Підставляємо це значення в наше рівняння у (-2) \u003d 12 - 8 + 1 \u003d 5. в результаті ми отримали позитивне число. це означає, що на проміжку від 1/3 до -1 функція зростає. Це, в свою чергу, означає, що на проміжках від міну з нескінченності до 1/3 і від -1 до плюс нескінченності функція спадає. Таким чином, можна зробити висновок, що число 1/3 - точка мінімуму функції на дослідженому проміжку, а -1 - точка максимуму.

Також варто відзначити, що на ЄДІ вимагають не просто знайти точки екстремуму, Але і провести з ними якусь операцію (додати, помножити і т.д.). Саме з цієї причини варто звернути особливу увагу на умови завдання. Адже через неуважність можна втратити бали.
функція y \u003d f (x) називається зростаючої (спадної) В деякому інтервалі, якщо при x 1< x 2 выполняется неравенство (f (x 1) < f (x 2) (f (x 1) > f (x 2)).
Якщо диференційована функція y \u003d f (x) на відрізку зростає (спадає), то її похідна на цьому відрізку f " (x)> 0
(f "(X)< 0).
Крапка x про називається точкою локального максимуму (мінімуму) Функції f (x), якщо існує околиця точки x про , Для всіх точок якої вірно нерівність f (x)≤ f (x о) (f (x)≥ f (x о)).
Точки максимуму і мінімуму називаються точками екстремуму, А значення функції в цих точках - її екстремумами.
точки екстремуму
Необхідні умови екстремуму . якщо точка x про є точкою екстремуму функції f (x), то або f " (x о) \u003d 0, або f(x о) не існує. Такі точки називають критичними, причому сама функція в критичній точці визначена. Екстремуми функції слід шукати серед її критичних точок.
Перше достатня умова. нехай x про - критична точка. Якщо f " (x) при переході через точку x про змінює знак плюс на мінус, то в точці x про функція має максимум, в іншому випадку - мінімум. Якщо при переході через критичну точку похідна не змінює знак, то в точці x про екстремуму немає.
Друге достатня умова.
Нехай функція f (x) має
f " (x) в околі точки x
про
і другу похідну f "" (x 0) в самій точці x про . Якщо f "(x про) \u003d 0, f "" (x 0)\u003e 0 (f "" (x 0)<0), то точка x про є точкою локального мінімуму (максимуму) функції f (x). Якщо ж f "" (x 0) \u003d 0, то потрібно або користуватися першим достатньою умовою, або залучати вищі.
На відрізку функція y \u003d f (x) може досягати найменшого або найбільшого значення або в критичних точках, або на кінцях відрізка.
Приклад 3.22.
Рішення.Так як f " (
Завдання на знаходження екстремуму функції
Приклад 3.23. a
Рішення. x і y y
0
≤ x≤
\u003e 0, а при x\u003e a / 4 S " < 0, значит, в точке x=a
/4 функция S имеет максимум. Значение
функції кв.
од).
Приклад 3.24.p ≈
Рішення.p p
S "
R \u003d 2, Н \u003d 16/4 \u003d 4.
Приклад 3.22.Знайти екстремуми функції f (x) \u003d 2x 3 - 15x 2 + 36x - 14.
Рішення.Так як f " (x) \u003d 6x 2 - 30x +36 \u003d 6 (x -2) (x - 3), то критичні точки функції x 1 \u003d 2 і x 2 \u003d 3. Екстремуми можуть бути тільки в цих точках. Так як при переході через точку x 1 \u003d 2 похідна змінює знак плюс на мінус, то в цій точці функція має максимум. При переході через точку x 2 \u003d 3 похідна змінює знак мінус на плюс, тому в точці x 2 \u003d 3 у функції мінімум. Зрозумівши значення функції в точках
x 1 \u003d 2 і x 2 \u003d 3, знайдемо екстремуми функції: максимум f (2) \u003d 14 і мінімум f (3) \u003d 13.
Приклад 3.23.Потрібно побудувати прямокутну майданчик біля кам'яної стіни так, щоб з трьох сторін вона була відгороджена дротяною сіткою, а четвертою стороною примикала до стіни. Для цього є a погонних метрів сітки. При якому співвідношенні сторін майданчик матиме найбільшу площу?
Рішення.Позначимо сторони майданчика через x і y . Площа майданчика дорівнює S \u003d xy. нехай y - це довжина сторони, що примикає до стіни. Тоді за умовою повинно виконуватися рівність 2x + y \u003d a. Тому y \u003d a - 2x і S \u003d x (a - 2x), де
0
≤ x≤ a / 2 (довжина і ширина площадки не можуть бути негативними).S "\u003d a - 4x, a - 4x \u003d 0 при x \u003d a / 4, звідки
y \u003d a - 2 × a / 4 \u003d a / 2. оскільки x \u003d a / 4 - єдина критична точка, перевіримо, чи змінюється знак похідної при переході через цю точку. При x a / 4 S "\u003e 0, а при x\u003e a / 4 S " < 0, значит, в точке x=a
/4 функция S имеет максимум. Значение
функції S (a / 4) \u003d a / 4 (a - a / 2) \u003d a 2/8 (кв.
од).
Оскільки S неперервна на і її значення на кінцях S (0) і S (a / 2) дорівнюють нулю, то знайдене значення буде найбільшим значенням функції. Таким чином, найбільш вигідним співвідношенням сторін майданчика за даних умов задачі є y \u003d 2x.
Приклад 3.24.Потрібно виготовити закритий циліндричний бак місткістю V \u003d 16p ≈ 50 м 3. Якими мають бути розміри бака (радіус R і висота Н), щоб на його виготовлення пішло найменшу кількість матеріалу?
Рішення.Площа повної поверхні циліндра дорівнює S \u003d 2p R (R + Н). Ми знаємо обсяг циліндра V \u003dp R 2 Н Þ Н \u003d V / p R 2 \u003d 16 p / p R 2 \u003d 16 / R 2. Значить, S (R) \u003d 2p (R 2 + 16 / R). Знаходимо похідну цієї функції:
S "(R) \u003d 2 p (2R- 16 / R 2) \u003d 4 p (R- 8 / R 2). S " (R) \u003d 0 при R 3 \u003d 8, отже,
R \u003d 2, Н \u003d 16/4 \u003d 4.
Визначення 1. Точка М (x 0; у 0) називається точкою максимуму (мінімуму) функції z \u003d f (x; y), якщо існує околиця точки М, така, що для всіх точок (x; y) з цієї околиці виконується нерівність:
f (x 0; y 0) f (x; y),.
теорема 1
(Необхідна умова існування екстремуму)
. Якщо диференційована функція z \u003d f (x; y) досягає екстремуму в точці М (x 0; y 0), то її приватні похідні першого порядку в цій точці дорівнюють нулю, тобто  ;
;
Точки, в яких приватні похідні дорівнюють нулю, називаються стаціонарнимиабо критичними точками.
теорема 2 (Достатня умова існування екстремуму)
Нехай функція z \u003d f (x; y):
а) визначена в деякому околі точки (x 0; y 0), в якій  і
і  ;
;
б) має в цій точці безперервні приватні похідні другого порядку
 ;
;


Тоді, якщо \u003d АС B 2\u003e 0, то в точці (x 0; y 0) функція z \u003d f (x; y) має екстремум, причому, якщо А< 0 (или С < 0) – максимум, если А > 0 (або С\u003e 0) - мінімум. У разі \u003d АС В 2< 0, функция z = f(x; y) экстремума не имеет. Если = AC B 2 = 0, то требуется дальнейшее исследование (сомнительный случай).
Приклад 1. Знайти екстремум функції z \u003d x 2 + xy + y 2 3x 6y.
Рішення. Знайдемо приватні похідні першого порядку:


Скористаємося необхідною умовою існування екстремуму:


Вирішуючи систему рівнянь, знаходимо координати x і y стаціонарних точок: x \u003d 0; y \u003d 3, т. е. М (0; 3).
Обчислимо приватні похідні другого порядку і знайдемо їх значення в точці М.
А \u003d  \u003d 2; С \u003d
\u003d 2; С \u003d  = 2;
= 2;
В \u003d  .
.
Складемо дискриминант \u003d АС В 2 \u003d 2 2 1\u003e 0, A \u003d 2\u003e 0. Отже, в точці М (0; 3) задана функція має мінімум. Значення функції в цій точці z min \u003d 9.
Знайти екстремуми функцій
322. z \u003d x 2 + y 2 + xy 4x 5y 323. z \u003d y 3 x 3 3xy
324. z \u003d x 2 2xy + 4y 3 325. z \u003d  y 2 x + 6y
y 2 x + 6y
326. z \u003d x y (1 x y) 327. z \u003d 2xy 4x 2y
328. z \u003d e x / 2 (x + y 2) 329. z \u003d x 3 + 8y 3 6xy + 1
330. z \u003d 3x 2 y x 3 y 4 331. z \u003d 3x + 6y x 2 xy + y 2
Найбільше і найменше значення функції двох змінних у замкненій області
Для того, щоб знайти найбільше і найменшезначення функції в замкненій області, треба:
1) знайти критичні точки, розташовані в даній області, і обчислити значення функції в цих точках;
2) знайти критичні точки на кордоні області і обчислити найбільше і найменше значення функцій в них;
3) з усіх знайдених значень вибрати найбільше і найменше.
Приклад 2. Знайти найбільше і найменше значення функції z \u003d  в колі x 2 + y 2 1.
в колі x 2 + y 2 1.
Рішення. Знайдемо координати критичних точок, розташованих усередині даної області, для чого обчислимо приватні похідні першого порядку функції z і прирівняємо їх до нуля.




звідки x \u003d 0, y \u003d 0 і, отже, М (0; 0) - критична точка.
Обчислимо значення функції z в точці М (0; 0): z (0; 0) \u003d 2.
Знайдемо критичні точки на кордоні області окружності, заданої рівнянням x 2 + y 2 \u003d 1. Підставляючи у 2 \u003d 1 x 2 в функцію z \u003d z (x; y), отримаємо функцію однієї змінної
z \u003d  ;
;
причому x [1; 1].
обчисливши похідну  і прирівнявши її нулю, отримаємо критичні точки на кордоні області x 1 \u003d 0, x 2 \u003d
і прирівнявши її нулю, отримаємо критичні точки на кордоні області x 1 \u003d 0, x 2 \u003d  , X 3 \u003d
, X 3 \u003d 
Знайдемо значення функції z (x) \u003d  в критичних точках і на кінцях відрізка [1; 1]: z (0) \u003d;
в критичних точках і на кінцях відрізка [1; 1]: z (0) \u003d;  =;
=; ; z (1) \u003d; z (1) \u003d
; z (1) \u003d; z (1) \u003d 
Виберемо найбільше та найменше серед значень функції z в критичних точках, розташованих усередині і на кордоні кола.
Отже, z наиб. \u003d Z (0; 0) \u003d 2
Також можна сказати, що в цих точках змінюється напрямок руху функції: якщо функція перестає падати і починає рости - це точка мінімуму, навпаки - максимуму.
Мінімуми і максимуми разом називають екстремумами функції.
Іншими словами, всі п'ять точок, виділених на графіку вище, є екстремумами.
Завдяки цьому знайти ці точки не складає проблем, навіть якщо у вас немає графіка функції.
Увага! коли пишуть екстремуми або максимуми / мінімуми мають на увазі значення функції тобто \\ (Y \\). коли пишуть точки екстремумів або точки максимумів / мінімумів мають на увазі ікси в яких досягаються максимуми / мінімуми. Наприклад, на малюнку вище, \\ (- 5 \\) точка мінімуму (або точка екстремуму), а \\ (1 \\) - мінімум (або екстремум).
Як знайти точки екстремумів функції за графіком похідної (7 завдання ЄДІ)?
Давайте разом знайдемо кількість точок екстремуму функції за графіком похідної на прикладі:

У нас дано графік - значить шукаємо в яких точках на графіку похідна дорівнює нулю. Очевидно, це точки \\ (- 13 \\), \\ (- 11 \\), \\ (- 9 \\), \\ (- 7 \\) і \\ (3 \\). Кількість точок екстремуму функції - \\ (5 \\).
Увага! Якщо дан графік похідною функції, а потрібно знайти точки екстремумів функції, Ми не вважаємо максимуми і мінімуми похідною! Ми вважаємо точки, в яких похідна функції звертається в нуль (тобто перетинає вісь \\ (x \\)).

Як знайти точки максимумів або мінімумів функції за графіком похідної (7 завдання ЄДІ)?
Щоб відповісти на це питання, потрібно згадати ще два важливих правил:
- Похідна позитивна там, де функція зростає.
- Похідна негативна там, де функція спадає.
За допомогою цих правил давайте знайдемо на графіку похідною точки мінімуму і максимуму функції.

Зрозуміло, що мінімуми і максимуми треба шукати серед точок екстремумів, тобто серед \\ (- 13 \\), \\ (- 11 \\), \\ (- 9 \\), \\ (- 7 \\) і \\ (3 \\).
Щоб простіше було вирішувати задачу розставимо на малюнку спочатку знаки плюс і мінус, що позначають знак похідної. Потім стрілки - позначають зростання, спадання функції.

Почнемо з \\ (- 13 \\): до \\ (- 13 \\) похідна позитивна тобто функція зростає, після - похідна негативна тобто функція падає. Якщо це уявити, то стає ясно, що \\ (- 13 \\) - точка максимуму.
\\ (- 11 \\): похідна спочатку позитивна, а потім негативна, це свідчить про те зростає, а потім зменшується. Знову спробуйте це подумки намалювати і вам стане очевидно, що \\ (- 11 \\) - це мінімум.
\\ (- 9 \\): функція зростає, а потім зменшується - максимум.
\\ (- 7 \\): мінімум.
\\ (3 \\): максимум.
Все вищесказане можна узагальнити наступними висновками:
- Функція має максимум там, де похідна дорівнює нулю і змінює знак з плюса на мінус.
- Функція має мінімум там, де похідна дорівнює нулю і змінює знак з мінуса на плюс.
Як знайти точки максимумів і мінімумів якщо відома формула функції (12 завдання ЄДІ)?
Щоб відповісти на це питання, потрібно робити все те ж, що і в попередньому пункті: знаходити де похідна позитивна, де негативна і де дорівнює нулю. Щоб було зрозуміліше напишу алгоритм з прикладом рішення:
- Знайдіть похідну функції \\ (f "(x) \\).
- Знайдіть корені рівняння \\ (f "(x) \u003d 0 \\).
- Намалюйте вісь \\ (x \\) і відзначте на ній точки отримані в пункті 2, покажіть дугами проміжки, на які розбивається вісь. Підпишіть над віссю \\ (f "(x) \\), а під віссю \\ (f (x) \\).
- Визначте знак похідної в кожному проміжку (методом інтервалів).
- Поставте знак похідної в кожному проміжку (над віссю), а стрілкою вкажіть зростання (↗) або спадання (↘) функції (під віссю).
- Визначте, як змінився знак похідної при переході через точки, отримані в пункті 2:
- якщо \\ (f '(x) \\) змінила знак з «\\ (+ \\)» на «\\ (- \\)», то \\ (x_1 \\) - точка максимуму;
- якщо \\ (f '(x) \\) змінила знак з «\\ (- \\)» на «\\ (+ \\)», то \\ (x_3 \\) - точка мінімуму;
- якщо \\ (f '(x) \\) не змінила знак, то \\ (x_2 \\) - може бути точкою перегину.

Усе! Точки максимумів і мінімумів знайдені.
Зображуючи на осі точки в яких похідна дорівнює нулю - масштаб можна не враховувати. Поведінка функції можна показати так, як це зроблено на малюнку нижче. Так буде очевидніше де максимум, а де мінімум.

приклад(ЄДІ). Знайдіть точку максимуму функції \\ (y \u003d 3x ^ 5-20x ^ 3-54 \\).
Рішення:
1. Знайдемо похідну функції: \\ (y "\u003d 15x ^ 4-60x ^ 2 \\).
2. Дорівняємо її до нуля і вирішимо рівняння:
\\ (15x ^ 4-60x ^ 2 \u003d 0 \\) \\ (|: 15 \\)
\\ (X ^ 4-4x ^ 2 \u003d 0 \\)
\\ (X ^ 2 (x ^ 2-4) \u003d 0 \\)
\\ (X \u003d 0 \\) \\ (x ^ 2-4 \u003d 0 \\)
\\ (X \u003d ± 2 \\)
3. - 6. Нанесемо точки на числову вісь і визначимо, як змінюється знак похідної та як рухається функція:

Тепер очевидно, що точкою максимуму є \\ (- 2 \\).
відповідь. \(-2\).
У завданнях оптимізації виникає необхідність знайти екстремуми функції двох і більше змінних за умови, що існує зв'язок між змінними зв'язку з цим, задана рівнянням ![]() . У цьому випадку говорять, що потрібно знайти умовний екстремум
.
. У цьому випадку говорять, що потрібно знайти умовний екстремум
.
Для того щоб знайти умовний екстремум потрібно знаходити приватні похідні і вирішувати системи рівнянь Існує алгоритм знаходження умовного екстремуму з трьох кроків, який зараз і розберемо на прикладі, і геометричний сенс умовного екстремуму, який повинен дійти до кожного при розборі цього самого прикладу.
Отже, алгоритм, який розберемо на прикладі найпоширенішою завдання - знаходження умовного екстремуму функції двох змінних. .
Крок 1. вводиться функція Лагранжа
де перший доданок - сама початкова функція, а другий доданок зі знаком мінус - ліва частина рівняння умови зв'язку, помножена на (лямбда) - множник Лагранжа.
Приклад 1.знайти умовні екстремуми функції двох змінних, що виражає площу прямокутника через його боку x і y за умови, що означає, що існує мотузка, якою можна обмежити цей прямокутник, і довжина цієї мотузки дорівнює 100.
Крок 1. Рішення. Наведемо рівняння умови зв'язку до необхідного виду з нулем в правій частині:
![]() .
.
складемо функцію Лагранжа:
Крок 2. Складаємо систему рівнянь з рівності приватних похідних нулю і уравенную умови зв'язку (необхідний ознака існування умовного екстремуму):
Рішення цієї системи рівнянь є точками можливого умовного екстремуму - стаціонарними точками або, як ще кажуть, критичними точками.
Приклад 1. Крок 2.
Рішення.

x і y :
Підставами ці вирази в третє рівняння і знайдемо значення множника Лагранжа:

x і y і знайдемо значення змінних вихідної функції:
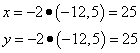
Отримали і. Ці значення є також координатами стаціонарної точки. Таким чином, отримали стаціонарну точку.
Крок 3. Нехай є стаціонарною точкою, знайденої на кроці 2. Щоб визначити, чи є умовний екстремум мінімумом або максимумом, потрібно знайти другий диференціал функції Лагранжа
![]()
і в отриманому виразі підставити замість "лямбда" її значення (значення множника Лагранжа), знайдені на кроці 2.
Якщо значення другого диференціала функції Лагранжа менше нуля (), то стаціонарна точка є точкою максимуму, якщо більше нуля (), то стаціонарна точка є точкою мінімуму. Якщо значення другого диференціала функції Лагранжа дорівнює нулю, то потрібні додаткові дослідження, але такі випадки практично не трапляються в задачах, що задаються студентам.
Координати стаціонарних точок підставляються в вихідну точку і, таким чином, ми остаточно знаходимо умовні екстремуми (Або мінімум і максимум або щось одне з цих екстремумів).
Приклад 1. Крок 3.
Рішення. Знайдемо другий диференціал функції Лагранжа:
![]()
У нашому випадку, так як перше і третє складові дорівнюють нулю, нам не доведеться підставляти в них значення множника Лагранжа. Зате потрібно знайти відносини між диференціалами dx і dy :

Так як отримані значення - протилежні за знаком, то отримуємо, що в будь-якому випадку.
Тепер можемо знайти значення умовного екстремуму вихідної функції, що є максимумом:
![]() .
.
Це задана вихідної функцією максимальна площа прямокутника, який можна обмежити мотузкою, довжина якої дорівнює 100.
Приклад 2.знайти умовні екстремуми
Крок 1. складемо функцію Лагранжа:
Крок 2. Знайдемо приватні похідні функції Лагранжа і складемо з їх рівності нулю і рівняння умови зв'язку систему рівнянь:

З першого і другого рівнянь висловимо відповідно x і y :

Підставами ці вирази в третє рівняння і знайдемо значення множника Лагранжа:

Підставами тепер значення множника Лагранжа в вирази для x і y і знайдемо значення змінних вихідної функції при двох значеннях множника Лагранжа:

Ці значення ікси і Ігрека є координатами двох стаціонарних точок. Таким чином, отримали стаціонарні точки ![]() .
.
Крок 3. Знайдемо приватні похідні другого порядку функції Лагранжа:
Знайдемо другий диференціал функції Лагранжа по формулі
![]() :
:
![]()
Отримали значення, менше нуля, отже, точка - точка умовного максимуму:
![]() .
.
Встановимо знак другого диференціала функції Лагранжа при значенні множника Лагранжа:
![]()
Отримали значення, більше нуля, отже, точка - точка умовного мінімуму:
![]() .
.
Таким чином, умовні екстремуми заданої функції знайдені.
Приклад 3.знайти умовні екстремуми функції двох змінних за умови.
Крок 1. складемо функцію Лагранжа:
Крок 2. Знайдемо приватні похідні функції Лагранжа і складемо з їх рівності нулю і рівняння умови зв'язку систему рівнянь:

З першого і другого рівнянь висловимо відповідно x і y :

Отримуємо, що, однак підстановка цих значень змінних в третє рівняння системи не дає вірного рівності. Тому вважаємо, що насправді другий співмножник рівності дорівнює нулю:. Звідси отримуємо
Шукаємо координати стаціонарних точок при значенні множника Лагранжа. Тоді з виразів для ікси і Ігрека з системи рівнянь слід, що. З третього рівняння системи отримуємо.