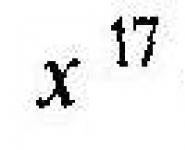Що таке безперервна випадкова величина. Випадкової величини. Диференціальна функція розподілу НСВ
Перевіримо, чи виконується вимога рівномірної обмеженості дисперсії. Напишемо закон розподілу 
:
|
|
|
|
|
|
|
Знайдемо математичне сподівання 
:
знайдемо дисперсію 
:
Ця функція зростає, отже, щоб обчислити константу, що обмежує дисперсію, можна обчислити межа:
Таким чином, дисперсії заданих випадкових величин необмежені, що й треба було довести.
Б) З формулювання теореми Чебишева слід, що вимога рівномірної обмеженості дисперсій є достатнім, але не необхідною умовою, тому не можна стверджувати, що до даної послідовності цю теорему застосувати не можна.
Послідовність незалежних випадкових величин Х 1, Х 2, ..., Х n, ... задана законом розподілу
D (X n) \u003d M (X n 2) - 2,
зважай, що M (X n) \u003d 0, знайдемо (викладки надаються виконати читачеві)
Тимчасово припустимо, що n змінюється безперервно (щоб підкреслити це припущення, позначимо n через х), і досліджуємо на екстремум функцію φ (х) \u003d х 2/2 х-1.
Прирівнявши першу похідну цієї функції до нуля, знайдемо критичні точки х 1 \u003d 0 і х 2 \u003d ln 2.
Відкинемо першу точку як що не представляє інтересу (n не приймає значення, рівного нулю); легко бачити, що в точок х 2 \u003d 2 / ln 2 функція φ (х) має максимум. З огляду на, що 2 / ln 2 ≈ 2.9 і що N - ціле позитивне число, обчислимо дисперсію D (X n) \u003d (n 2/2 n -1) α 2 для найближчих до числа 2.9 (ліворуч і праворуч) цілих чисел, т . Е. для n \u003d 2 і n \u003d 3.
При n \u003d 2 дисперсія D (X 2) \u003d 2α 2, при n \u003d 3 дисперсія D (Х 3) \u003d 9 / 4α 2. очевидно,
(9/4) α 2\u003e 2α 2.
Таким чином, найбільша можлива дисперсія дорівнює (9/4) α 2, тобто дисперсії випадкових величин Х n рівномірно обмежені числом (9/4) α 2.
Послідовність незалежних випадкових величин X 1, X 2, ..., X n, ... задана законом розподілу
Чи можна застосувати до заданої послідовності теорема Чебишева?
Зауваження. Оскільки випадкові величини Х, однаково розподілені і незалежні, то читач, знайомий з теоремою Хинчина, може обмежитися обчисленням лише математичного очікування і переконатися, що воно скінчилося.
Оскільки випадкові величини Х n незалежні, то вони поготів і попарно незалежні, тобто перша вимога теореми Чебишева виконується.
Легко знайти, що M (X n) \u003d 0, т.е.первое вимога кінцівки математичних очікувань виконується.
Залишається перевірити здійснимість вимоги рівномірної обмеженості дисперсій. За формулою
D (X n) \u003d M (X n 2) - 2,
зважай, що M (X n) \u003d 0, знайдемо
Таким чином, найбільша можлива дисперсія дорівнює 2, тобто дисперсії випадкових величин Х n рівномірно обмежені числом 2.
Отже, всі вимоги теореми Чебишева виконуються, отже, до розглянутої послідовності ця теорема застосовна.
Знайти ймовірність того, що в результаті випробування величина Х прийме значення, укладену в інтервалі (0, 1/3).
Випадкова величина Х задана на всій осі Ох функцією розподілена F (x) \u003d 1/2 + (arctg x) / π. Знайти ймовірність того, що в результаті випробування величина Х прийме значення, укладену в інтервалі (0, 1). Імовірність того, що Х прийме значення, укладену в інтервалі (a, b), дорівнює приросту функції розподілу на цьому інтервалі: P (a Р (0<
Х <1) = F(1)-F(0)
= x =1 -
x =0
= 1/4 Випадкова величина Х функцією розподілу Знайти ймовірність того, що в результаті випробування величина Х прийме значення, укладену в інтервалі (-1, 1). Імовірність того, що Х прийме значення, укладену в інтервалі (a, b), дорівнює приросту функції розподілу на цьому інтервалі: P (a Р (-1<
Х <1) = F(1)-F(-1)
= x =-1
– x =1
= 1/3. Функція розподілу неперервної випадкової величини Х (часу безвідмовної роботи деякого пристрою) дорівнює F (х) \u003d 1-е х / T (х≥0). Знайти ймовірність безвідмовної роботи пристрою за час х≥Т. Імовірність того, що Х прийме значення, укладену в інтервалі x≥T, дорівнює приросту функції розподілу на цьому інтервалі: P (0 P (x≥T) \u003d 1 - P (T Випадкова величина Х задана функцією розподілу Знайти ймовірність того, що в результаті випробування Х прийме значення: а) менше 0.2; б) менше трьох; в) менше трьох; р) котрі менше п'яти. а) Так як при х≤2 функція F (х) \u003d 0, то F (0, 2) \u003d 0, тобто P (х< 0, 2)=0; б) Р (Х< 3) = F(3) = x =3
= 1.5-1 = 0.5; в) події Х≥3 і Х<3 противоположны,
поэтому Р(Х≥3)+Р(Х<3)=1. Отсюда, учитывая,
что Р(Х<3)=0.5 [см. п. б.], получим Р(Х≥3) =
1-0.5 = 0.5; г) сума ймовірностей протилежних подій дорівнює одиниці, тому Р (Х≥5) + Р (Х<5)=1. Отсюда, используя условие,
в силу которого при х>4 функція F (x) \u003d 1, отримаємо Р (Х≥5) \u003d 1-Р (Х<5) = 1-F(5)
= 1-1 = 0. Випадкова величина Х задана функцією распределнія Знайти ймовірність того, що в результаті чотирьох незалежних випробувань величина Х рівно три рази прийме значення, що належить інтервалу (0.25, 0.75). Імовірність того, що Х прийме значення, укладену в інтервалі (a, b), дорівнює приросту функції розподілу на цьому інтервалі: P (a P (0.25< X <0.75) =
F(0.75)-F(0.25) =
0.5 Отже,, або Випадкова величина X задана на всій осі Ox функцією розподілу. Знайти можливе значення, яке задовольняє умові: з ймовірністю випадкова X в результаті випробування прийме значення більше Рішення. Події і - протіволожность, тому. Отже,. Так як, то. За визначенням функції розподілу,. Отже,, або Дискретна випадкова величина X задана законом розподілу Отже, шукана функція розподілу має вигляд Дискретна випадкова величина X задана законом розподілу Знайти функцію розподілу і накреслити її графік. Дана функція розподілу неперервної випадкової величини X Знайти щільність розподілу f (x). Щільність розподілу дорівнює першої похідної від функції розподілу: Безперервна випадкова величина X задана щільністю розподілу в інтервалі; поза цим інтервалом. Знайти ймовірність того, що X прийме значення, що належить інтервалу. Скористаємося формулою. За умовою, і. Отже, шукана ймовірність Безперервна випадкова величина X задана щільністю розподілу Скористаємося формулою. За умовою, і Щільність розподілу неперервної випадкової величини Х в інтервалі (-π / 2, π / 2) дорівнює f (x) \u003d (2 / π) * cos2x; поза цим інтервалом f (x) \u003d 0. Знайти ймовірність того, що в трьох незалежних випробуваннях Х прийме рівно два рази значення, укладену в інтервалі (0, π / 4). Скористаємося формулою Р (a Р (0 Відповідь: π + 24π. fx \u003d 0, при x≤0cosx, при 0 використовуємо формулу Якщо х ≤0, то f (x) \u003d 0, отже, F (x) \u003d - ∞00dx \u003d 0. якщо 0 F (x) \u003d - ∞00dx + 0xcosxdx \u003d sinx. Якщо x≥ π2, то F (x) \u003d - ∞00dx + 0π2cosxdx + π2x0dx \u003d sinx | \u200b\u200b0π2 \u003d 1. Отже, шукана функція розподілу Fx \u003d 0, при x≤0sinx, при 0 Задана щільність розподілу неперервної випадкової величини Х: Fx \u003d 0, при x≤0sinx, при 0 Знайти функцію розподілу F (x). використовуємо формулу Щільність розподілу неперервної випадкової величини Х задана на всій осі Ох равеством. Знайти постійний параметр С. Таким чином, Щільність розподілу неперервної випадкової величини задана на всій осі рівністю Знайти постійний параметр С. Рішення. Щільність розподілу повинна задовольняти умові. Вимагатимемо, щоб ця умова виконувалася для заданої функції: Знайдемо спочатку невизначений інтеграл: Потім обчислимо невласний інтеграл: Таким чином, Підставивши (**) в (*), остаточно отримаємо. Щільність розподілу неперервної випадкової величини X в інтервалі дорівнює; поза цим інтервалом f (х) \u003d 0. Знайти постійний параметр С. Знайдемо спочатку невизначений інтеграл: Потім обчислимо невласний інтеграл: Підставивши (**) в (*), остаточно отримаємо. Щільність розподілу неперервної випадкової величини Х задана в інтервалі рівністю; поза цим інтервалом f (х) \u003d 0. Знайти постійний параметр С. Рішення. Щільність розподілу повинна задовольняти умові, але так як f (x) поза інтервалу дорівнює 0 досить, щоб вона задовольняла: Знайдемо спочатку невизначений інтеграл: Потім обчислимо невласний інтеграл: Підставивши (**) в (*), остаточно отримаємо. Випадкова величина X задана щільністю розподілу ƒ (x) \u003d 2x в інтервалі (0,1); поза цим інтервалом ƒ (x) \u003d 0. Знайти математичне сподівання величини X. Р Підставивши a \u003d 0, b \u003d 1, ƒ (x) \u003d 2x, отримаємо Відповідь: 2/3. Випадкова величина X задана щільністю розподілу ƒ (x) \u003d (1/2) x в інтервалі (0; 2); поза цим інтервалом ƒ (x) \u003d 0. Знайти математичне сподівання величини X. Р Підставивши a \u003d 0, b \u003d 2, ƒ (x) \u003d (1/2) x, отримаємо М (Х) \u003d Відповідь: 4/3. Випадкова величина X в інтервалі (-с, с) задана щільністю розподілу ƒ Р Підставивши a \u003d -с, b \u003d c, ƒ (x) \u003d, отримаємо З огляду на, що підінтегральна функція непарна і межі інтегрування симетричні відносно початку координат, робимо висновок, що інтеграл дорівнює нулю. Отже, М (Х) \u003d 0. Цей результат можна отримати одразу, якщо взяти до уваги, що крива розподілу симетрична відносно прямої х \u003d 0. Випадкова величина Х в інтервалі (2, 4) задана щільністю розподілу f (x) \u003d Випадкова величина Х в інтервалі (3, 5) задана щільністю розподілу f (x) \u003d Рішення. Уявімо щільність розподілу у вигляді Випадкова величина Х в інтервалі (-1, 1) задана щільністю розподілу випадковою величиною
називається змінна, яка може приймати ті чи інші значення в залежності від різних обставин, і випадкова величина називається неперервною
, Якщо вона може приймати будь-яке значення з будь-якого обмеженого або необмеженого інтервалу. Для неперервної випадкової величини неможливо вказати всі можливі значення, тому позначають інтервали цих значень, які пов'язані з певними можливостями. Прикладами безперервних випадкових величин можуть служити: діаметр деталі, обточувати до заданого розміру, зріст людини, дальність польоту снаряда і ін. Так як для безперервних випадкових величин функція F(x), на відміну від дискретних випадкових величин , Ніде не має стрибків, то ймовірність будь-якого окремого значення неперервної випадкової величини дорівнює нулю. Це означає, що для неперервної випадкової величини безглуздо говорити про розподіл ймовірностей між її значеннями: кожне з них має нульову ймовірність. Однак в деякому сенсі серед значень неперервної випадкової величини є "більш і менш ймовірні". Наприклад, навряд чи у кого-небудь виникне сумнів, що значення випадкової величини - зростання навмання зустрінутого людини - 170 см - більш ймовірно, ніж 220 см, хоча і одне, і інше значення можуть зустрітися на практиці. В якості закону розподілу, що має сенс тільки для безперервних випадкових величин, вводиться поняття щільності розподілу або щільності ймовірності. Підійдемо до нього шляхом порівняння сенсу функції розподілу для неперервної випадкової величини і для дискретної випадкової величини. Отже, функцією розподілу випадкової величини (як дискретної, так і безперервної) або інтегральної функцією називається функція, яка визначає ймовірність, що значення випадкової величини X менше або дорівнює граничному значенню х. Для дискретної випадкової величини в точках її значень x1
, x2
, ..., xi, ... зосереджені маси ймовірностей p1
, p2
, ..., pi, ..., Причому сума всіх мас дорівнює 1. Перенесемо цю інтерпретацію на випадок неперервної випадкової величини. Уявімо собі, що маса, рівна 1, що не зосереджена в окремих точках, а безперервно "розмазана" по осі абсцис Оx з якоюсь нерівномірною щільністю. Ймовірність влучення випадкової величини на будь-яку ділянку Δ x буде інтерпретуватися як маса, яка припадає на цю ділянку, а середня щільність на цій ділянці - як відношення маси до довжини. Тільки що ми ввели важливе поняття теорії ймовірностей: щільність розподілу. щільністю ймовірності f(x) Неперервної випадкової величини називається похідна її функції розподілу: Знаючи функцію щільності, можна знайти ймовірність того, що значення неперервної випадкової величини належить закритому інтервалу [ a; b]: ймовірність того, що неперервна випадкова величина X ухвалить будь-яке значення з інтервалу [ a; b], Дорівнює визначеному інтегралу від її щільності ймовірності в межах від a до b: При цьому загальна формула функції F(x) Розподілу ймовірностей неперервної випадкової величини, якою можна користуватися, якщо відома функція щільності f(x)
: Графік щільності ймовірності неперервної випадкової величини називається її кривої розподілу (рис. Нижче). Площа фігури (на малюнку заштрихована), обмеженої кривою, прямими, проведеними з точок a і b перпендикулярно осі абсцис, і віссю Ох, Графічно відображає ймовірність того, що значення неперервної випадкової величини Х знаходиться в межах від a до b. 1. Імовірність того, що випадкова величина прийме будь-яке значення з інтервалу (і площа фігури, яку обмежують графік функції f(x) І вісь Ох) Дорівнює одиниці: 2. Функція щільності ймовірності не може приймати негативні значення: а за межами існування розподілу її значення дорівнює нулю щільність розподілу f(x), Як і функція розподілу F(x), Є однією з форм закону розподілу, але на відміну від функції розподілу, вона не універсальна: щільність розподілу існує тільки для безперервних випадкових величин. Згадаємо про двох найважливіших в практиці видах розподілу неперервної випадкової величини. Якщо функція щільності розподілу f(x) Неперервної випадкової величини в деякому кінцевому інтервалі [ a; b] Приймає постійне значення C, А за межами інтервалу приймає значення, рівне нулю, то таке розподіл називається рівномірним . Якщо графік функції щільності розподілу симетричний відносно центру, середні значення зосереджені поблизу центру, а при віддаленні від центру збираються більш відрізняються від середніх (графік функції нагадує розріз дзвони), то таке розподіл називається нормальним . Приклад 1. Відома функція розподілу ймовірностей неперервної випадкової величини: знайти функцію f(x) Щільності ймовірності неперервної випадкової величини. Побудувати графіки обох функцій. Знайти ймовірність того, що неперервна випадкова величина прийме будь-яке значення в інтервалі від 4 до 8:. Рішення. Функцію щільності ймовірності отримуємо, знаходячи похідну функції розподілу ймовірностей: Графік функції F(x) - парабола: Графік функції f(x) - пряма: Знайдемо ймовірність того, що неперервна випадкова величина прийме будь-яке значення в інтервалі від 4 до 8: Приклад 2. Функція щільності ймовірності неперервної випадкової величини дана в вигляді: обчислити коефіцієнт C . знайти функцію F(x) Розподілу ймовірностей неперервної випадкової величини. Побудувати графіки обох функцій. Знайти ймовірність того, що неперервна випадкова величина прийме будь-яке значення в інтервалі від 0 до 5:. Рішення. коефіцієнт C знайдемо, користуючись властивістю 1 функції щільності ймовірності: Таким чином, функція щільності ймовірності неперервної випадкової величини: Інтегруючи, знайдемо функцію F(x) Розподілу ймовірностей. якщо x < 0
, то
F(x) \u003d 0. якщо 0< x < 10
, то x \u003e 10, то F(x) = 1
. Таким чином, повний запис функції розподілу ймовірностей: Графік функції f(x)
: Графік функції F(x)
: Знайдемо ймовірність того, що неперервна випадкова величина прийме будь-яке значення в інтервалі від 0 до 5: Приклад 3.Щільність ймовірності неперервної випадкової величини X задана рівністю, при цьому. знайти коефіцієнт А, Ймовірність того, що неперервна випадкова величина X ухвалить будь-яке значення з інтервалу] 0, 5 [, функцію розподілу неперервної випадкової величини X. Рішення. За умовою приходимо до рівності Отже,, звідки. Отже, Тепер знаходимо ймовірність того, що неперервна випадкова величина X ухвалить будь-яке значення з інтервалу] 0, 5 [: Тепер отримаємо функцію розподілу даної випадкової величини: Приклад 4.Знайти щільність ймовірності неперервної випадкової величини X, Яка приймає тільки невід'ємні значення, а її функція розподілу Нехай неперервна випадкова величина Х задана функцією розподілу f (x). Припустимо, що всі можливі значення випадкової величини належать відрізку [ a, b]. Визначення. математичним очікуваннямнеперервної випадкової величини Х, можливі значення якої належать відрізку, називається певний інтеграл Якщо можливі значення випадкової величини розглядаються на всій числовій осі, то математичне очікування перебувають розслідування щодо формулі: При цьому, звичайно, передбачається, що невласний інтеграл сходиться. Визначення. дисперсією неперервної випадкової величини називається математичне сподівання квадрата її відхилення. За аналогією з дисперсією випадкової величини, для практичного обчислення дисперсії використовується формула: Визначення. Середнім квадратичним відхиленнямназивається квадратний корінь з дисперсії. Визначення. модоюМ 0 дискретної випадкової величини називається її найбільш ймовірне значення. Для неперервної випадкової величини мода - таке значення випадкової величини, при якій щільність розподілу має максимум. Якщо багатокутник розподілу для дискретної випадкової величини або крива розподілу для неперервної випадкової величини має два або кілька максимумів, то такий розподіл називається двухмодальним або многомодальним. Якщо розподіл має мінімум, але не має максимуму, то воно називається антімодальним. Визначення. медианой M D випадкової величини Х називається таке її значення, щодо якого равновероятно отримання більшого або меншого значення випадкової величини. Геометрично медіана - абсциса точки, в якій площа, обмежена кривою розподілу ділиться навпіл. Відзначимо, що якщо розподіл одномодальних, то мода і медіана збігаються з математичним очікуванням. Визначення. початковим моментомпорядку kвипадкової величини Х називається математичне очікування величини Х k. Початковий момент першого порядку дорівнює математичному очікуванню. Визначення. центральним моментомпорядку k випадкової величини Х називається математичне очікування величини Для дискретної випадкової величини:. Для неперервної випадкової величини:. Центральний момент першого порядку завжди дорівнює нулю, а центральний момент другого порядку дорівнює дисперсії. Центральний момент третього порядку характеризує асиметрію розподілу. Визначення.
Ставлення центрального моменту третього порядку до середньому квадратичному відхиленню в третього ступеня називається коефіцієнтом асиметрії. Визначення.
Для характеристики гостровершинності і плосковершінних розподілу використовується величина, звана ексцесом. Крім розглянутих величин використовуються також так звані абсолютні моменти: Абсолютний початковий момент:. Абсолютний центральний момент:. Абсолютний центральний момент першого порядку називається середнім арифметичним відхиленням. Приклад. Для розглянутого вище прикладу визначити математичне очікування і дисперсію випадкової величини Х. Приклад. В урні 6 білих і 4 чорних кулі. З неї п'ять разів поспіль витягують кулю, причому кожен раз вийнятий кулю повертають назад і кулі перемішують. Прийнявши за випадкову величину Х число витягнутих білих куль, скласти закон розподілу цієї величини, визначити її математичне сподівання і дисперсію. Оскільки кулі в кожному досвіді повертаються назад і перемішуються, то випробування можна вважати незалежними (результат попереднього досвіду не впливає на ймовірність появи або непоявленія події в іншому досвіді). Таким чином, ймовірність появи білої кулі в кожному досвіді постійна і дорівнює Таким чином, в результаті п'яти послідовних випробувань біла куля може не з'явитися зовсім, з'явитися один раз, два, три, чотири або п'ять разів. Для написання закону розподілу треба знайти ймовірності кожного з цих подій. 1) Біла куля не з'явилося зовсім: 2) Білий куля з'явилася один раз: 3) Біла куля з'явитися два рази:. Як відомо, випадковою величиною
називається змінна величина, яка може приймати ті чи інші значення в залежності від випадку. Випадкові величини позначають великими літерами латинського алфавіту (X, Y, Z), а їх значення - відповідними малими літерами (x, y, z). розрізняють безперервні і дискретні випадкові величини
. Безперервною випадковою величиною
називається випадкова величина Х, якщо її функція розподілу (інтегральна функція розподілу) подана в вигляді: функція f(x) називається щільністю розподілу ймовірностей випадкової величини
X (диференціальної функцією розподілу). імовірність
того, що неперервна випадкова величина X приймає значення в заданому проміжку, обчислюється таким чином: Приклади розподілів ймовірностей неперервної випадкової величини Х: При вирішенні завдань широко використовують числові характеристики неперервних випадкових величин (таблиця 1). Завдання.
Відома щільність ймовірності випадкової величини: Знайти: а) параметр а; б) функцію розподілу F (x); в) ймовірність попадання X в інтервал (-π / 4; π / 4). Рішення.
1. Знаючи властивості щільності ймовірності - функції f (х), знайдемо невідомий параметр а. З нерівності f (х) ≥0, робимо висновок, що а≥0. далі: Обчислимо даний інтеграл. Знаючи, що його значення має дорівнювати одиниці, висловимо а. А - (- а) \u003d 2а. Знаючи, що отримуємо 2а \u003d 1, звідси а \u003d 1/2. якщо х ≤ 0 якщо 0< х ≤ π, то \u003d ½ (-cosx + cos0) \u003d ½ (1-cosx) Якщо х\u003e π, то Шукана інтегральна функція приймає остаточний вигляд: Графік функції F (x) представлений на малюнку 2. 3. Ймовірність влучення випадкової величини Х в інтервал (-π / 4; π / 4) знайдемо за формулою: P (a ВИПАДКОВІ ВЕЛИЧИНИ Приклад 2.1. Випадкова величина X задана функцією розподілу Знайти ймовірність того, що в результаті випробування X прийме значення, укладені в проміжку (2,5; 3,6). Рішення: Х в проміжок (2,5; 3,6) можна визначити двома способами: Приклад 2.2. При яких значеннях параметрів А і В функція F(x) \u003d A + Be - x може бути функцією розподілу для невід'ємних значень випадкової величини Х. Рішення: Так як всі можливі значення випадкової величини Хналежать інтервалу, то для того, щоб функція була функцією розподілу для Х, Має виконуватися властивість: відповідь: Приклад 2.3. Випадкова величина X задана функцією розподілу Знайти ймовірність того, що в результаті чотирьох незалежних випробувань величина X рівно 3 рази прийме значення, що належить інтервалу (0,25; 0,75). Рішення:Ймовірність влучення величини Х в проміжок (0,25; 0,75) знайдемо за формулою: Приклад 2.4. Ймовірність влучення м'ячем у кошик при одному кидку дорівнює 0,3. Скласти закон розподілу числа влучень при трьох кидках. Рішення: Випадкова величина Х - число влучень у кошик при трьох кидках - може приймати значення: 0, 1, 2, 3. Імовірність того, що Х Х: Приклад 2.5. Два стрільці роблять по одному пострілу в мішень. Ймовірність влучення в неї першим стрільцем дорівнює 0,5, другим - 0,4. Скласти закон розподілу числа влучень в мішень. Рішення: Знайдемо закон розподілу дискретної випадкової величини Х - числа влучень в мішень. Нехай подія - влучення в мішень першим стрільцем, а - потрапляння другим стрільцем, і - відповідно їх промахи. Складемо закон розподілу ймовірностей СВ Х: Приклад 2.6. Випробовуються 3 елементи, які працюють незалежно один від одного. Тривалості часу (в годинах) безвідмовної роботи елементів мають функції щільності розподілу: для першого: F 1 (t) =1-e - 0,1 t, Для другого: F 2 (t) = 1-e - 0,2 t, Для третього: F 3 (t) =1-e - 0,3 t. Знайти ймовірність того, що в інтервалі часу від 0 до 5 годин: відмовить тільки один елемент; відмовлять тільки два елементи; відмовлять всі три елементи. Рішення: Скористаємося визначенням виробляє функції ймовірностей: Імовірність того, що в незалежних випробуваннях, в першому з яких ймовірність появи події Адорівнює, в другому і т. д., подія Аз'явиться рівно раз, дорівнює коефіцієнту при в розкладанні виробляє функції за ступенями. Знайдемо ймовірності відмови і неотказ відповідно першого, другого і третього елемента в інтервалі часу від 0 до 5 годин: Складемо виробляє функцію: Коефіцієнт при дорівнює ймовірності того, що подія Аз'явиться рівно три рази, тобто ймовірності відмови всіх трьох елементів; коефіцієнт при дорівнює ймовірності того, що відмовлять рівно два елементи; коефіцієнт при дорівнює ймовірності того, що відмовить тільки один елемент. Приклад 2.7. Дана щільність ймовірності f(x) Випадкової величини X: Знайти функцію розподілу F (x). Рішення: Використовуємо формулу: Таким чином, функція розподілу має вигляд: Приклад 2.8. Пристрій складається з трьох незалежно працюючих елементів. Імовірність відмови кожного елемента в одному досвіді дорівнює 0,1. Скласти закон розподілу числа відмовили елементів в одному досвіді. Рішення: Випадкова величина Х - число елементів, які відмовили в одному досвіді - може приймати значення: 0, 1, 2, 3. Імовірність того, що Х прийме ці значення, знайдемо за формулою Бернуллі: Таким чином, отримуємо наступний закон розподілу ймовірностей випадкової величини Х: Приклад 2.9. У партії з 6 деталей є 4 стандартних. Навмання відібрано 3 деталі. Скласти закон розподілу числа стандартних деталей серед відібраних. Рішення:Випадкова величина Х - число стандартних деталей серед відібраних - може приймати значення: 1, 2, 3 і має гипергеометрическое розподіл. Ймовірності того, що Х де --
число деталей в партії; --
число стандартних деталей в партії; –
число відібраних деталей; --
число стандартних деталей серед відібраних. Приклад 2.10. Випадкова величина має щільність розподілу причому і не відомі, але, а й. Знайдіть і. Рішення: В даному випадку випадкова величина X має трикутний розподіл (розподіл Сімпсона) на відрізку [ a, b]. числові характеристики X: отже, відповідь: Приклад 2.11. В середньому по 10% договорів страхова компанія виплачує страхові суми у зв'язку з настанням страхового випадку. Обчислити математичне сподівання і дисперсію числа таких договорів серед навмання вибраних чотирьох. Рішення:Математичне сподівання і дисперсію можна знайти за формулами: Можливі значення СВ (число договорів (з чотирьох) з настанням страхового випадку): 0, 1, 2, 3, 4. Використовуємо формулу Бернуллі, щоб обчислити ймовірності різного числа договорів (з чотирьох), за якими були виплачені страхові суми: Ряд розподілу СВ (число договорів з настанням страхового випадку) має вигляд: Відповідь:,. Приклад 2.12. З п'яти троянд дві білі. Скласти закон розподілу випадкової величини, що виражає число білих троянд серед двох одночасно взятих. Рішення:У вибірці з двох троянд може або не виявитися білої троянди, або може бути одна або дві білі троянди. Отже, випадкова величина Х може приймати значення: 0, 1, 2. Вірогідність того, що Х прийме ці значення, знайдемо за формулою: де --
число троянд; --
число білих троянд; –
число одночасно взятих троянд; --
число білих троянд серед узятих. Тоді закон розподілу випадкової величини буде такою: Приклад 2.13. Серед 15 зібраних агрегатів 6 потребують додаткової мастилі. Скласти закон розподілу числа агрегатів, які потребують додаткового мастилі, серед п'яти навмання вибраних із загального числа. Рішення:Випадкова величина Х - число агрегатів, які потребують додаткового мастилі серед п'яти обраних - може приймати значення: 0, 1, 2, 3, 4, 5 і має гипергеометрическое розподіл. Ймовірності того, що Х прийме ці значення, знайдемо за формулою: де --
число зібраних агрегатів; --
число агрегатів, які потребують додаткового мастилі; –
число обраних агрегатів; --
число агрегатів, які потребують додаткового мастилі серед обраних. Тоді закон розподілу випадкової величини буде такою: Приклад 2.14. З надійшли в ремонт 10 годині 7 потребують загальної чищенні механізму. Годинник не розсортовані по виду ремонту. Майстер, бажаючи знайти годинник, які потребують чищення, розглядає їх по черзі і, знайшовши такий годинник, припиняє подальший перегляд. Знайти математичне сподівання і дисперсію числа переглянутих годин. Рішення: Випадкова величина Х - число агрегатів, які потребують додаткового мастилі серед п'яти обраних - може приймати значення: 1, 2, 3, 4. Вірогідність того, що Х прийме ці значення, знайдемо за формулою: Тоді закон розподілу випадкової величини буде такою: Тепер обчислимо числові характеристики величини: Відповідь:,. Приклад 2.15. Абонент забув останню цифру потрібного йому номера телефону, проте пам'ятає, що вона непарна. Знайти математичне сподівання і дисперсію числа зроблених їм наборів номера телефону до потрапляння на потрібний номер, якщо останню цифру він набирає навмання, а набрану цифру в подальшому не набирає. Рішення: Випадкова величина може приймати значення:. Так як набрану цифру абонент надалі не набирає, то ймовірності цих значень рівні. Складемо ряд розподілу випадкової величини: Обчислимо математичне сподівання і дисперсію числа спроб набору номера: Відповідь:,. Приклад 2.16. Імовірність відмови за час випробувань на надійність для кожного приладу серії дорівнює p. Визначити математичне сподівання числа приладів, що дали відмову, якщо випробування піддалися N приладів. Рішення:Дискретна випадкова величина X - число відмовили приладів в N незалежних випробуваннях, в кожному з яких ймовірність появи відмови дорівнює p,розподілена за біноміальним законом. Математичне сподівання біноміального розподілу дорівнює добутку числа випробувань на ймовірність появи події в одному випробуванні: Приклад 2.17. Дискретна випадкова величина X приймає 3 можливих значення: з ймовірністю; з ймовірністю і з ймовірністю. Знайти і, знаючи, що M ( X) = 8. Рішення: Використовуємо визначення математичного очікування і закону розподілу дискретної випадкової величини: Знаходимо:. Приклад 2.18. Відділ технічного контролю перевіряє вироби на стандартність. Імовірність того, що виріб стандартно, дорівнює 0,9. У кожній партії міститься 5 виробів. Знайти математичне сподівання випадкової величини X - числа партій, в кожній з яких міститься рівно 4 стандартних вироби, якщо перевірці підлягають 50 партій. Рішення: В даному випадку всі проведені досліди незалежні, а ймовірності того, що в кожній партії міститься рівно 4 стандартних вироби, однакові, отже, математичне очікування можна визначити за формулою: де - число партій; Імовірність того, що в партії міститься рівно 4 стандартних вироби. Імовірність знайдемо за формулою Бернуллі: відповідь: Приклад 2.19. Знайти дисперсію випадкової величини X - числа появ події A в двох незалежних випробуваннях, якщо ймовірність появи події в цих випробуваннях однакові і відомо, що M(X) = 0,9. Рішення: Завдання можна вирішити двома способами. 1) Можливі значення СВ X : 0, 1, 2. За формулою Бернуллі визначимо ймовірності цих подій: ,
Тоді закон розподілу X має вид: З визначення математичного очікування визначимо ймовірність: Знайдемо дисперсію СВ X: 2) Можна використовувати формулу: відповідь: Приклад 2.20. Математичне сподівання і середнє квадратичне відхилення нормально розподіленої випадкової величини X відповідно рівні 20 і 5. Знайти ймовірність того, що в результаті випробування X прийме значення, укладену в інтервалі (15; 25). Рішення: Ймовірність влучення нормальної випадкової величини Х на ділянку від до виражається через функцію Лапласа: Приклад 2.21. Дана функція: При якому значенні параметра C ця функція є щільністю розподілу деякої неперервної випадкової величини X? Знайти математичне очікування і дисперсію випадкової величини X. Рішення:Для того, щоб функція була щільністю розподілу деякої випадкової величини, вона повинна бути неотрицательна, і вона повинна задовольняти властивості: отже: Обчислимо математичне сподівання за формулою: Обчислимо дисперсію за формулою: T дорівнює p. Необхідно знайти математичне сподівання і дисперсію цієї випадкової величини. Рішення: Закон розподілу дискретної випадкової величини X - числа появ події в незалежних випробуваннях, в кожному з яких ймовірність появи події дорівнює, називають біноміальним. Математичне сподівання біноміального розподілу дорівнює добутку числа випробувань на ймовірність появи події А одному випробуванні: Приклад 2.25. Проводиться три незалежних пострілу по мішені. Ймовірність влучення при кожному пострілі дорівнює 0.25. Визначити середнє відхилення числа влучень при трьох пострілах. Рішення: Так як виробляється три незалежних випробування, і ймовірність появи події А (попадання) в кожному випробуванні однакова, то будемо вважати, що дискретна випадкова величина X - число влучень в мішень - розподілена за біноміальним законом. Дисперсія біноміального розподілу дорівнює добутку числа випробувань на ймовірності появи і непоявленія події в одному випробуванні: Приклад 2.26. Середнє число клієнтів, які відвідують страхову компанію за 10 хв., Дорівнює трьом. Знайти ймовірність того, що в найближчі 5 хвилин прийде хоча б один клієнт. Середнє число клієнтів, які прийшли за 5 хвилин: Приклад 2.29. Час очікування заявки в черзі на процесор підпорядковується показовому закону розподілу із середнім значенням 20 секунд. Знайти ймовірність того, що чергова (довільна) заявка буде очікувати процесор більше 35 секунд. Рішення: У цьому прикладі математичне очікування Тоді шукана ймовірність: Приклад 2.30. Група студентів у кількості 15 осіб проводить збори в залі, в якому 20 рядів по 10 місць у кожному. Кожен студент займає місце в залі випадковим чином. Яка ймовірність того, що не більше трьох осіб знаходитимуться на сьомому місці ряду? Рішення: Приклад 2.31. Тоді відповідно до класичного визначення ймовірності: де --
число деталей в партії; --
число нестандартних деталей в партії; –
число відібраних деталей; --
число нестандартних деталей серед відібраних. Тоді закон розподілу випадкової величини буде такою.
Звідси, або.
. Звідси, або.
При x \u003d 0 похідна не існує.
в інтервалі; поза цим інтервалом. Знайти ймовірність того, що X прийме значення, що належить інтервалу.
. Отже, шукана ймовірність
.
. (*)
.
.
. (*)
.
.
. (*)
(**)
Вимагатимемо, щоб ця умова виконувалася для заданої функції:
.
. (*)
(**)
ешеніем. використовуємо формулу
ешеніем. використовуємо формулу
=
4/3
(X) \u003d; поза цим інтервалом ƒ (x) \u003d 0. Знайти математичне сподівання величини X.
ешеніем. використовуємо формулу
. Звідси видно, що при х \u003d 3 щільність розподілу досягає максимуму; отже,. Крива розподілу симетрична відносно прямої х \u003d 3, тому і.
; поза цим інтервалом f (x) \u003d 0. Знайти моду, математичне очікування і медіану величини Х.
. Звідси видно, що при х \u003d 3 щільність розподілу досягає максимуму; отже,. Крива розподілу симетрична відносно прямої х \u003d 4, тому і.
; поза цим інтервалом f (x) \u003d 0. Знайти: а) моду; б) медіану Х.Функція розподілу неперервної випадкової величини і щільність ймовірності
.
.
.
Властивості функції щільності ймовірності неперервної випадкової величини
.
.
. Таблиця 1 - Числові характеристики неперервних випадкових величин
числова характеристика Позначення і формула
Математичне очікування
Якщо всі можливі значення Х належать інтервалу (а, b), то математичне сподівання обчислюють
дисперсія
неперервної випадкової величини Х
інакше
Якщо всі можливі значення Х належать інтервалу (а, b), то дисперсію обчислюють
інакше
Середнє квадратичне відхилення
неперервної випадкової величини Х
Приклад рішення задачі по темі «Безперервні випадкові величини»
Побудувати графіки f (x), F (x).
P (-π / 4< x < π/4) = F(π/4) - F(-π/4) = ½ (1-cos π/4) – 0 = ½ (1-½√2).
.
.
.
.
.
.
. Вирішуючи цю систему, отримаємо дві пари значень:. Так як за умовою завдання, то остаточно маємо: 
. .
.
.
0,6561
0,2916
0,0486
0,0036
0,0001
.
.
.
.
.
.
.
.
.
.
.
.
.
0,2
,
.
,
.
.
.
.
.
. .
. .
, А інтенсивність відмов дорівнює.
